|
Presentation Page 2
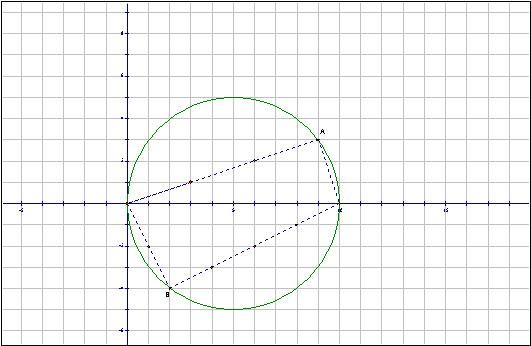
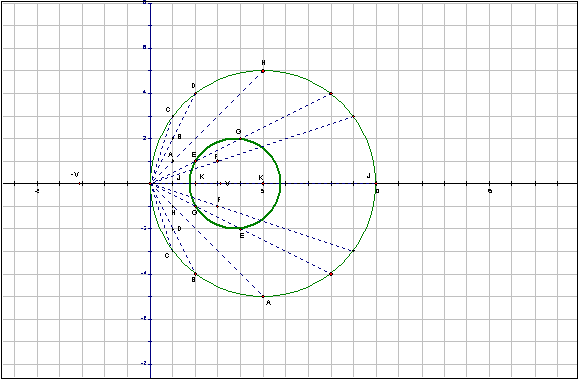
Lattice point A gives us one factorization of 10: (3 + 1i)(3 - 1i). Lattice point B gives us two factorizations of 10: (1 - 2i)(2 + 4i) and (2 - 4i)(1 + 2i).
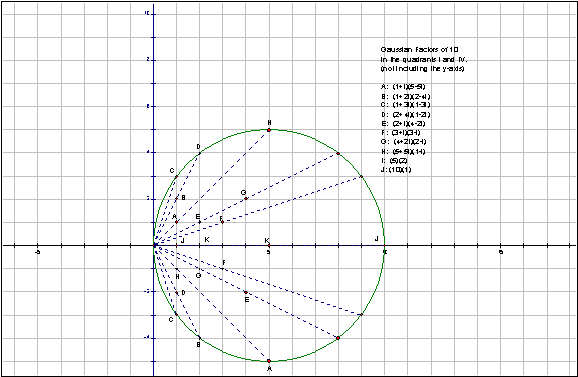
The Gaussian integer factor pairs of 10. The Gaussian factors will lie on chords from the origin to the lattice points on the circle.
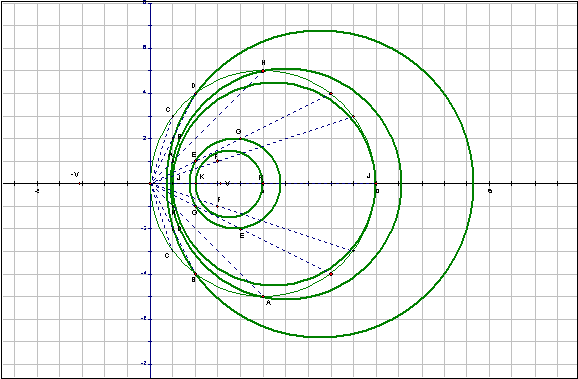
The factor pairs 1 + 1i and 5 - 5i lie on a circle, centered on the y-axis, through ± sqrt 10
So does EVERY PAIR OF FACTORS!! (What about the integer factors?)
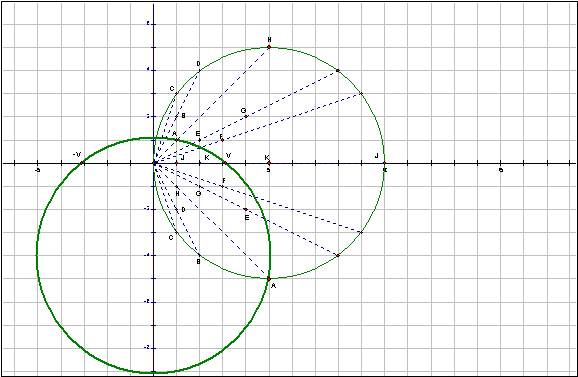
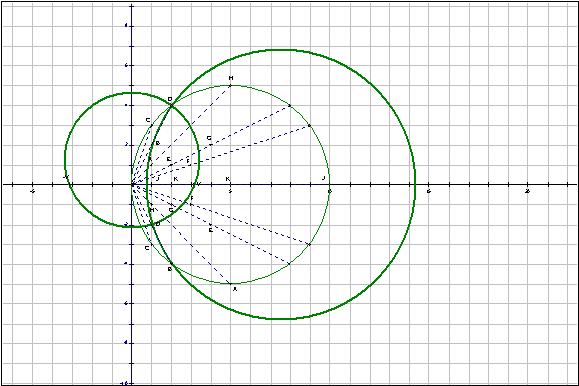
Factor pairs E and G are conjugates of each other. There is a circle through these four points. The roots of 10 are INVERSE POINTS with respect to the circle.
This is true of almost every quartet of congugate factor pairs. What about factor pairs C and F?
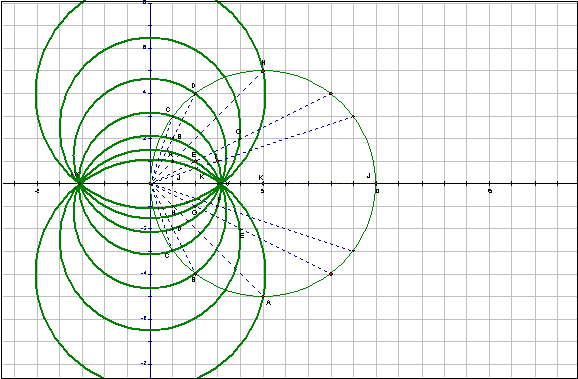
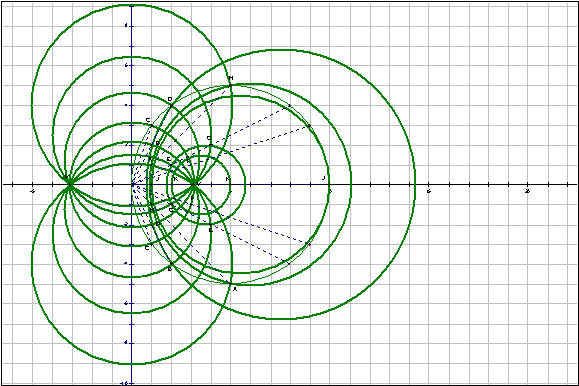
Here are the two families of circle together at last! Every Gaussian factor pair will be the intersection of two circles (one from each family). Below is an example of pair D.
|