|
Paper Cup Mathematics - Directions for the Teacher Download files in PDF format: papercup.pdf Concepts: Geometry, Measurement
Grade Level: 8-12
Description: Imagine a discarded paper cup rolling on its side of a flat surface. What geometric shape does the path of the cup form? Students investigate this question and begin the activity by experimenting with paper cups. They devise methods to draw the path of the cup, which may include a compass and straightedge construction. The activity concludes with a problem that requires finding the area of a carousel platform. Student Worksheet 2 includes an investigation using Geometer's Sketchpad®. Directions: Demonstrate the situation of rolling a paper cup on its side on a flat surface to the class. Ask students to formulate a conjecture about the path of the cup. Distribute Worksheet 1, paper cups, and chart paper to groups of students and set the task to determine the geometric shape formed by the rolling cup as pictured in Figure 1. Figure 1: A rolling paper cup and its path
Some groups may need help getting started. If so, suggest that they start rolling the paper cup on one edge of their chart paper and try to determine the path. When the cup is taken apart at (or cut along) its seam and flattened out, the cup may look like the cup in the photo of Figure 2. Figure 2. Photo of the "side" of a flattened paper cup with the bottom removed
Students can trace the shape over and over until the path that would be formed by the rolling cup is closed. Once students are convinced that the path is determined by two circles (the top and bottom rims of the cup) and the distance between them (the slant height), they should try a "proof by construction." To do this, they may use one flattened cup and, with their construction tools, draw two chords on an arc of the outer (or greater) circle and construct the perpendicular bisectors of the chords. Where the perpendicular bisectors of the chords intersect is the expected center of the concentric circles forming the original path. The diameters of the outer and inner circles may be measured and the area of the region between the circles can be estimated. After students have finished Worksheet 1, there are many other questions that you can pose for further investigation.
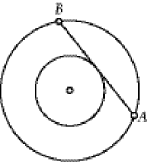
EXTENSION: A PUZZLE ABOUT ANNULI The following problem is adapted from a puzzler posed on Car Talk, a NPR radio show. For a complete discussion of the original problem, log onto The same problem was posed as the area of a lighthouse keeper's rug in "Creative Geometry Problems Can Lead to Creative Problem Solvers," by George A. Milauskas in Learning and Teaching Geometry, K-12, the 1987 Yearbook of the National Council of Teachers of Mathematics. Pose the following problem to your students. Their group was hired to paint the floor of a merry-go-round. They want to measure the area of the floor exactly because they do not want to buy extra paint. The carousel is circular and in the middle is a smaller circle that contains all the machinery for the carousel. Therefore, the carousel platform is an annulus. The only measurement provided is the length of the chord of the outer circle that is also tangent to the inner circle. (See Figure 3.) The measure of segment AB is 70 feet. Find the area of the annulus. Figure 3. Concentric circles with a chord of the greater tangent to the smaller
Ask students to simulate the Car Talk annulus problem using dynamic software such as Geometer's Sketchpad® Have them begin with a chord that remains constant when the center of the circles is dragged. Worksheet 2 details the steps of the construction. References Milauskus, George A. "Creative Geometry Problems Can Lead to Creative Problem Solvers," in Learning and Teaching Geometry, K-12, 1987 Yearbook of the National Council of Teachers of Mathematics (edited by Mary Montgomery Lindquist and Albert P. Shulte). Reston, VA: The Council, 1987, p. 77. Answers to Worksheet 1
Answer to the Problem of Car Talk and Worksheet 2 |