How many faces does the cube have? __________ edges?________ vertices?__________
Each face has ________________diagonals. Total face diagonals per cube? ______________________
Diagonal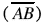 
and adjacent edges 
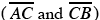form what type of geometric figure? _____________ Are all such figures of the cube congruent? ____________ Why? ________________________________________________________
Assuming an edge length of 2 units, calculate the length of each face diagonal._____________________
When 6 congruent square pyramids are put together with their apexes inward they form a cube as shown below. The non-base edges of the pyramids form the interior diagonals of the cube and are ______________ as long as a lateral edge of each pyramid.
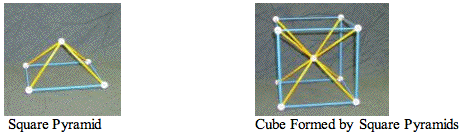
Look at the above diagram of the square pyramid and use the Pythagorean Theorem to find each length.
When the cube is surrounded by a jacket of 6 square pyramids, a new polyhedron is created. How many faces does it appear to have? ______________What are the measures of the dihedral angles formed where three faces meet at a vertex on the new polyhedron? _________________________
Show/explain with words or diagrams why the triangles of two adjacent pyramids create a flat rhombic face of the new polyhedron.
Use the diagrams below to help calculate the lengths of the long and short diagonals. You may also find the Zome™ tool model/straw model helpful.
The rhombic dodecahedron packs space. Put together several of the rhombic dodecahedrons to see this amazing property. Explain in words and/or diagrams why you think this works.
Show your calculations for each of the following.
Find the volume of the cube. ________________________
Find the volume of the square based pyramid using at least two techniques.
__________________________
Find the volume of the rhombic dodecahedron.
______________________________________________
